Compact and Semi-simple Lie algebras
I just read about (why I care about) compact and semi-simple lie algebras (again) and want to concentrate all my knowledge here. (Source: M Hamilton - Mathematical Gauge Theory (Springer))
This will go:
- Setup
- Semi-simple
- Compact
1. Setup
The main players are: a lie algebra \(\mathfrak g\), with its
- lie bracket \([X,Y]\),
- adjoint map \(\text{ad}_XY:= [X,Y]\),
- Killing form \(B(X,Y) = \text{tr}(\text{ad}_X\circ\text{ad}_Y)\).
In fact this list illustrates that there are 3 points of view on the same object \(\mathfrak g\).
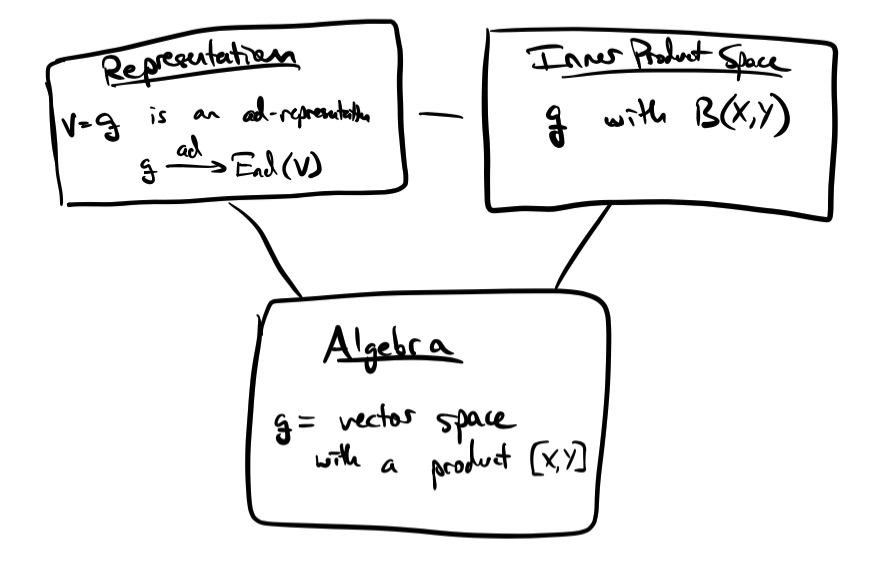
- Algebra: \(\mathfrak g\) is an “algebra”, i.e. a vector space with a product \([X,Y]\)
- Representation: \(V=\mathfrak g\) is a lie algebra representation of \(\mathfrak g\) itself via \(\text{ad}:\mathfrak g \to \text{End}(V)\)
- Inner Product (Metric) Space: \(\mathfrak g\) is a vector space with an “inner product” \(B\) (officially just a bilinear form \(B\), but we may justify treating it like an inner product).
To me, the order of most useful to least useful is 2-3-1. We will take view 1. as our foundation, define our terms in that setting, and then look at the translations in the other points of view.
For example
- An ideal is a subspace \(a\subset \mathfrak g\) such that \([\mathfrak g,a]\subset a\)
- In terms of a representation, an ideal is the same as a subrepresentation, because \(\text{ad}_{\mathfrak g} a \subset a\).
- The center is the ideal \(z:=\{X~,~[X,\mathfrak g]=0\}\)
- In terms of a representation, the center is the kernel of the representation map \(\mathfrak g \overset{\text{ad}}\longrightarrow \text{End}(V)\), because \(z=\{X~,~\text{ad}_X=0\}\)
- In terms of an innerproduct space, since \(\text{ad}_X=0\), we have \(B(X,\mathfrak g)=0\).
Thus we might guess that the center corresponds to the subspace of degenerate or null vectors (\(|X|=0\)). It turns out this is not quite true; the center is a possibly strict subspace of the degenerate subspace. Degeneracy will pair better with abelian ideals, where \([a,a]=0\). The center is an abelian ideal.
2. Semi-simple
- A simple lie algebra is one that is non-abelian and has no nontrivial ideals (trivial: \(0\) and \(\mathfrak g\)).
- In terms of a representation, the second condition is exactly that \(V\) is irreducible.
- A semi-simple lie algebra is one that has no nonzero abelian ideals.
- Notice we have: simple \(\implies\) semi-simple \(\implies\) non-abelian.
Semi-simple lie algebras can be broken into simple parts, as will be clear in the structure theorem below. The key fact for this theorem is the following;
Lemma (Cartan’s Criterion) Semi-simple \(\iff\) B is nondegenerate.
This translates the semi-simplicity property to the innerproduct space point of view. (This is what I meant earlier about connecting degeneracy with abelian ideals.)
Theorem (Semi-simple structure theorem) A semi-simple \(\mathfrak g\) decomposes \(B\)-orthogonally into simple ideals (aka irreducible components)
\[\begin{equation*} \mathfrak g = \mathfrak g_1 \oplus \dotsm \oplus \mathfrak g_n. \end{equation*}\]
Notice the connections between the different points of view of \(\mathfrak g\). We have simultaneously decomposed \(\mathfrak g\) into irreducible representations as well as orthogonal subspaces with respect to \(B\).
About the proof:
There is a similar, easier theorem in representation theory: if \(V\) is a representation with a representation-compatible (definite) innerproduct, then \(V\) can be decomposed orthogonally into irreducible components. The proof is just to keep splitting \(V\) into subrepresentations using orthogonal complements, until you hit irreducible factors everywhere.
Now, we want to do the same thing to prove the structure theorem, but \(B\) is only nondegenerate. This is of course strictly weaker than positive or negative definite. So when we take an orthogonal complement of a subspace \(a\), we a priori may have \(a\cap a^\perp \neq 0\). Not good for direct sums.
However, it turns out that \(a\cap a^\perp\) is an abelian ideal, so it is still \(0\) here! The previous method goes through.
3. Compact
A lie algebra is compact if it comes from a compact lie group. Now we are adding an additional structure / assumption to everything, and some properties become easier to see.
Remember how the center \(z\subset \mathfrak g\) didn’t exactly correspond to the degenerate subspace?
Theorem Compact \(\implies ~ B\leq 0\) (negative semi-definite) with \(|X|=0\) only for \(X\) in the center \(z\).
Thus the abelian ideal distinction is gone in the compact case. It seems that the only abelian ideal for compact algebras is the center.
More importantly, we have that compact lie algebras split as
\[\mathfrak g = z \oplus \mathfrak h.\]Here the \(\mathfrak h\) is just \(z^\perp\), and \(B\) is negative definite on this part.
In fact, for compact lie algebras: semi-simple \(\implies z=0 \implies B\) is negative definite \(\implies\) semi-simple.
Since compactness descends to \(\mathfrak h\), we have \(\mathfrak h\) is semi-simple, and thus
Theorem (Compact structure theorem) A compact \(\mathfrak g\) decomposes \(B\)-orthogonally into compact irreducible componenets
\[\begin{align*} \mathfrak g &= z \oplus \mathfrak h \\ &= \big(\mathfrak u(1)\oplus \dotsm \oplus \mathfrak u(1)\big) \oplus \big( \mathfrak g_1 \oplus \dotsm \oplus \mathfrak g_n \big) \\ \end{align*}\]
There are in fact only so many compact simple algebras (possibilities for \(\mathfrak g_i\)).
- \(\mathfrak{su}(n+1)\) for \(n\geq 1\)
- \(\mathfrak{so}(2n+1)\) for \(n\geq 2\)
- \(\mathfrak{sp}(n)\) for \(n\geq 3\)
- \(\mathfrak{so}(2n)\) for \(n\geq 4\)
- Exceptional types \(G_2,F_4,E_6,E_7,E_8\)
I don’t know anything about the exceptional types, but the \(n\) restrictions in the first four are mostly to avoid overcounting.